Matrices

ºDefinición: Una matriz es un arreglo bidimensional de números (llamados entradas de la matriz) ordenados en filas (o renglones) y columnas, donde una fila es cada una de las líneas horizontales de la matriz y una columna es cada una de las líneas verticales. A una matriz con n filas y m columnas se le denomina matriz n-por-m (escrito ) donde . El conjunto de las matrices de tamaño  se representa como , donde  es el campo al cual pertenecen las entradas. El tamaño de una matriz siempre se da con el número de filas primero y el número de columnas después.

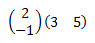
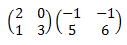
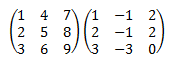
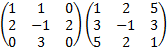
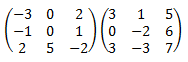
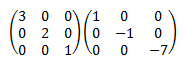
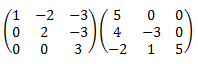
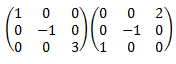
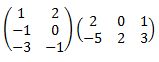
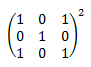
Dos matrices se dice que son iguales si tienen el mismo tamaño y los mismos elementos en las mismas posiciones.A la entrada de una matriz que se encuentra en la fila ${\displaystyle i-\,\!}$ésima y la columna ${\displaystyle j-\,\!}$ésima se le llama entrada ${\displaystyle i,j\,\!}$ o entrada ${\displaystyle (i,j)\,\!}$-ésimo de la matriz. En estas expresiones también se consideran primero las filas y después las columnas.

ºMatriz Simetrica:Una matriz es simétrica si es una matriz cuadrada, la cual tiene la característica de ser igual a su traspuesta. Una matriz de  elementos:

${\displaystyle A=\left[{\begin{array}{ccccccc}a_{11}&a_{12}&a_{13}&\cdots &a_{1m}\\a_{21}&a_{22}&a_{23}&\cdots &a_{2m}\\a_{31}&a_{32}&a_{33}&\cdots &a_{3m}\\\vdots &\vdots &\vdots &\ddots &\vdots \\a_{n1}&a_{n2}&a_{n3}&\cdots &a_{nm}\\\end{array}}\right]}$

es simétrica, si es una matriz cuadrada (m = n) y ${\displaystyle a_{ij}=a_{ji}}$ para todo i, j con i, j =1,2,3,4,...,n. Nótese que la simetría es respecto a la diagonal principal.

Ejemplo para n = 3:

${\displaystyle \left[{\begin{array}{rrr}-8&-1&3\\-1&7&4\\3&4&9\\\end{array}}\right]}$

A es también la matriz traspuesta de sí misma: ${\displaystyle A^{t}=A}$. Esta última igualdad es una definición alternativa de matriz simétrica. Las matrices simétricas son un caso particular de las matrices hermíticas.

ºMatriz Transpuesta:ea  una matriz con  filas y  columnas. La matriz transpuesta, denotada con .​

Está dada por:

${\displaystyle (A^{t})_{ij}=A_{ji},\ 1\leq i\leq n,\ 1\leq j\leq m}$

En donde el elemento ${\displaystyle a_{ji}}$ de la matriz original ${\displaystyle A}$ se convertirá en el elemento ${\displaystyle a_{ij}}$ de la matriz transpuesta ${\displaystyle A^{t}}$.

Ejemplos:

${\displaystyle {\begin{bmatrix}a&b\\c&d\end{bmatrix}}^{t}={\begin{bmatrix}a&c\\b&d\end{bmatrix}}}$

${\displaystyle {\begin{bmatrix}1&2\\3&4\\5&6\\\end{bmatrix}}^{t}={\begin{bmatrix}1&3&5\\2&4&6\end{bmatrix}}}$

Otro ejemplo un poco más grande es el siguiente:

${\displaystyle {\begin{bmatrix}0&0&4\\1&0&4\\0&1&0\\0&3&2\\0&2&3\\0&3&4\\3&3&1\end{bmatrix}}^{t}\quad =\quad {\begin{bmatrix}0&1&0&0&0&0&3\\0&0&1&3&2&3&3\\4&4&0&2&3&4&1\end{bmatrix}}}$

ºEjercicios Resueltos:

Producto 1

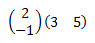
Ver Solución

Las dimensiones de las matrices son distintas: $2\times 1$ y $1\times 2$. Pero como el número de filas de una coincide con el número de columnas de la otra, pueden multiplicarse obteniendo una matriz cuadrada de dimensión 2.
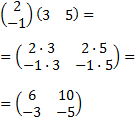
Calculamos el producto:

---

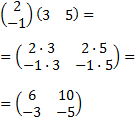
Producto 2

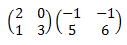
Ver Solución

Las matrices son cuadradas de dimensión 2, así que podemos multiplicarlas obteniendo una matriz de la misma dimensión:

---

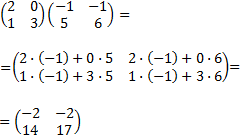
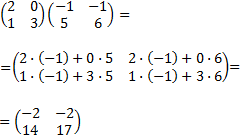
Producto 3

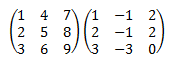
Ver Solución

Las matrices son cuadradas la misma dimensión: $3\times 3$.
Calculamos el producto:

---

Producto 4

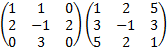
Ver Solución

El producto es

---

Producto 5

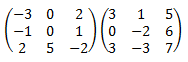
Ver Solución

Calculamos el producto:

---

Producto 6

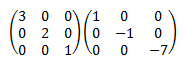
Ver Solución

Las matrices son cuadradas con la misma dimensión y diagonales y, por tanto, ya sabemos de antemano que su producto es una matriz diagonal:

---

Producto 7

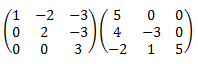
Ver Solución

La matriz de la izquierda es triangular superior y la de la derecha es triangular inferior. Como son "distintas", el producto no tiene porqué ser triangular:

---

Producto 8

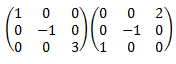
Ver Solución

Calculamos el producto:

---

Producto 9

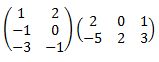
Ver Solución

El producto es

---

Producto 10

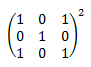
Ver Solución

Puesto que la potencia cuadrado de un elemento es multiplicarlo por sí mismo, calculamos la potencia de la matriz multiplicándola consigo misma.
Nota: para calcular potencias de matrices, éstas deben ser cuadradas ya que si la dimensión es $m\times n$, siendo $m\ne n$, no podremos calcular los productos.